Lending

As established in the AMM section, X (or Y) refers to the reserves of the supplied asset of a pool. Z refers to the interest per second of the pool. Depending on the spot price of the assets and the transition price of the pool, X (Token A) can be the supplied asset and Y (Token B) the collateral asset, or vice versa, in any case, the supplied asset will always be either X or Y (but not both of them).

Lending

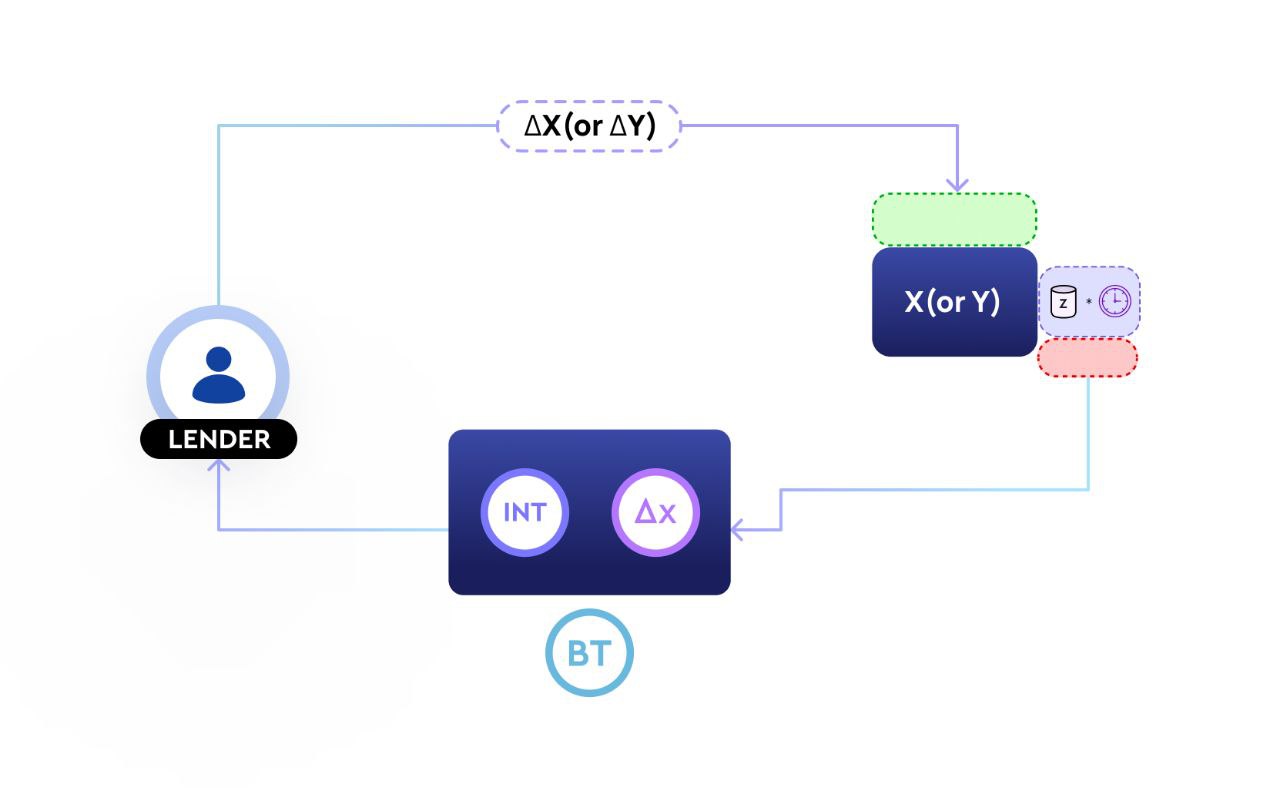
ΔX (or ΔY) represents the change in the pool's reserve of the supplied asset (i.e., the amount lent by lenders). ΔZ*d represents the change in the pool's reserve for the interest (i.e., the interest paid out to lenders).

Lenders lend the supplied asset to the AMM in exchange for interest.

In other words, lenders add X (or Y) to the AMM and remove Z*d from the AMM (representing the fixed interest to be earned from the AMM, at maturity).

A lend transaction is denoted by the following formula:

$$(X + Y + ΔX + ΔY)(Z - ΔZ) = K$$

The lent principal along with their interest is represented by an ERC-1155 token (called the Bond Token, BT). BT represents the claim to the underlying assets of the pool.

A lending transaction lowers the pool's interest rate for the next transactions. The larger the lent size relative to the available liquidity of the pool, the lower the interest rate for the next transactions will be. This is known as price impact. However, note that this does not affect the interest rate of borrowers/lenders prior to this transaction.

The exact calculations of the new interest rate (after a lending transaction) is as follows: $I = (Z +ΔZ)/(X+Y+ΔX+ΔY)$ Where,

• Z represents the original reserves of interest per second in the AMM

• ΔZ represents the change in interest per second (w.r.t. the AMM), which in this scenario, is negative

• X represents the original reserves of Token A in the AMM

• ΔX represents the change in Token A (w.r.t. the AMM), which in this scenario, is positive

• Y represents the original reserves of Token B in the AMM, which in this scenario, is zero

• ΔY represents the change in Token B (w.r.t. the AMM), which in this scenario, is zero

Thus, the pool's interest rate decreases as more lending happens.

NOTE: Interest amount is paid to the lenders irrespective of the borrow demand in a given pool. This is because Liquidity Providers become counterparty to all the transactions in the pool.

Closing a lend position

Closing after maturity

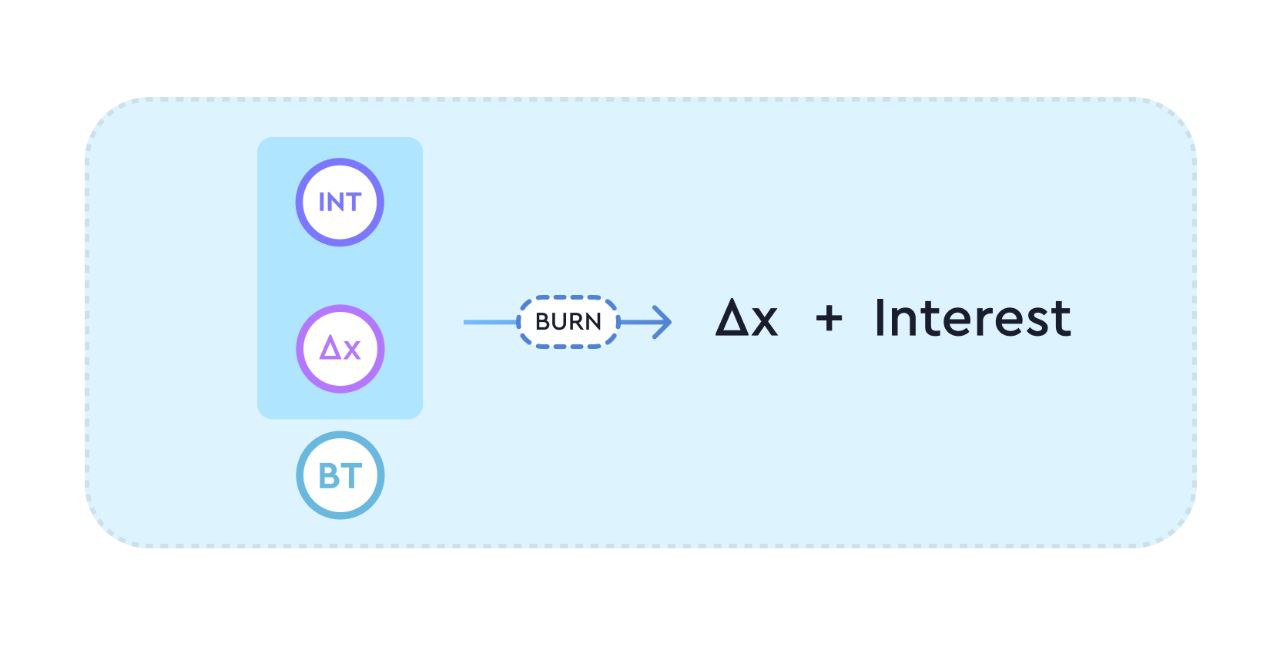
Lenders who close their lending positions after maturity will receive their full principal and interest by burning their BT.

Lenders will receive their principal and interest in the form of the underlying asset in the pool.

Closing before maturity

Timeswap, although defined as a fixed-term lending/borrowing protocol, allows users to exit their positions anytime before maturity.

The Z*d component stored in the lender's BT (representing the interest took from the AMM when opening the lend position) is added back to the AMM to remove X (or Y), representing the principal from the pool. As a result, after closing a lend position, the pool's interest rate will increase. A close lend transaction is denoted by the following formula:

$$(X + Y - ΔX - ΔY)(Z + ΔZ) = K$$

Note that closing their lending positions early does not yield interest in a pro-rated manner. The variables determining how much a lender will receive while closing their positions early is: 1) how long the lender have been lending for, 2) the interest rates at entry and exit, and 3) the amount of liquidity available at exit.

The longer the lender have been lending for, and the lower the interest rate at exit (relative to entry), the higher the proportion the lender will receive while closing early. Additionally, there is price impact based on the available liquidity.

Closing a lend position early is equal to opening a borrow transaction. Hence, it is ideal to close a lend transaction at interest rate lower than when it is opened.

Risks

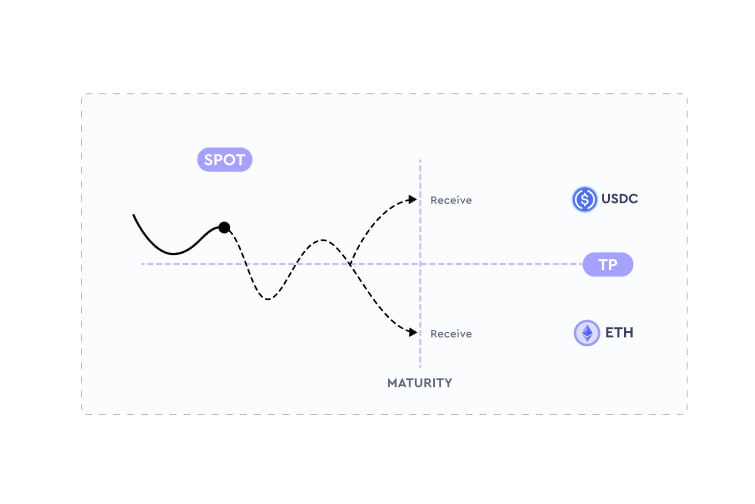
Lenders may not receive the asset they originally lent out in (e.g., lenders lent out USDC but receive ETH at maturity instead, as borrowers have defaulted).

As established in The AMM, the underlying asset in the pool can be either of the two tokens (either Token A or B), and changes based on the relationship of the transition price, external market price, and actions of arbitrageurs. Regardless of the outcome, the lenders will always receive the fixed interest.

The price level at which the optimal action (to repay or to default) of a borrower is expected to change is referred to as the transition price (TP). There is an emphasis on 'expected' since the price level does not take into account each borrower's debt (and whether they are rational actors based on the economic outcomes).