The AMM
The core mechanism of Timeswap
Timeswap utilises a Duration-Weighted Constant Sum Product Market Maker (DW-CSPMM) to enable the creation of permissionless lending/borrowing pools for any pair of ERC-20 tokens. Lenders, borrowers and liquidity providers (LPs) interact with the AMM, leading to the market's discovery of interest rates.
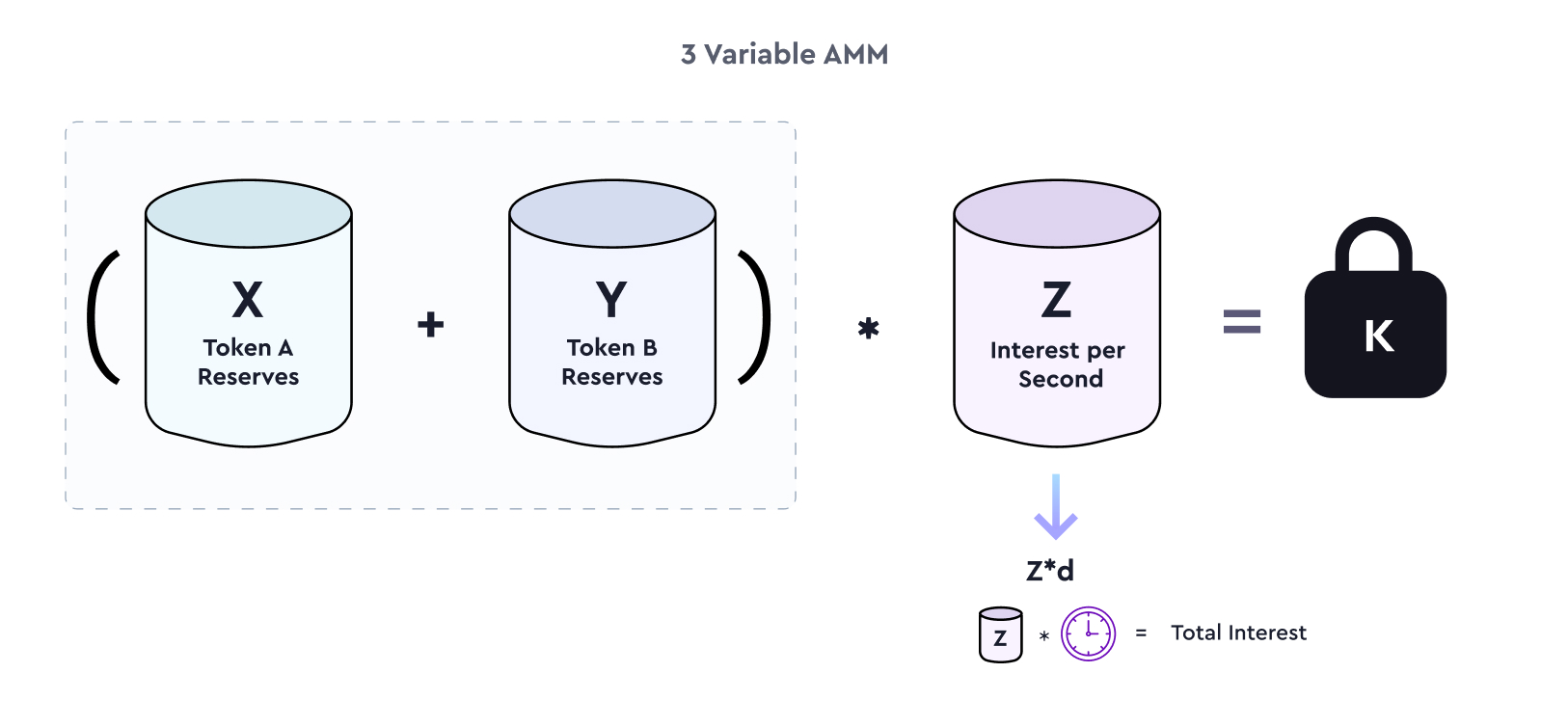
The formula for the AMM is as follows:
Where,
X represents the reserves of Token A in the AMM, deposited by lenders and LPs.
Y represents the reserves of Token B in the AMM, deposited by lenders and LPs.
Z represents the reserves of interest per second in the AMM, deposited by borrowers and LPs.
K is the Constant Sum Product invariant.
Another parameter that influences the AMM:
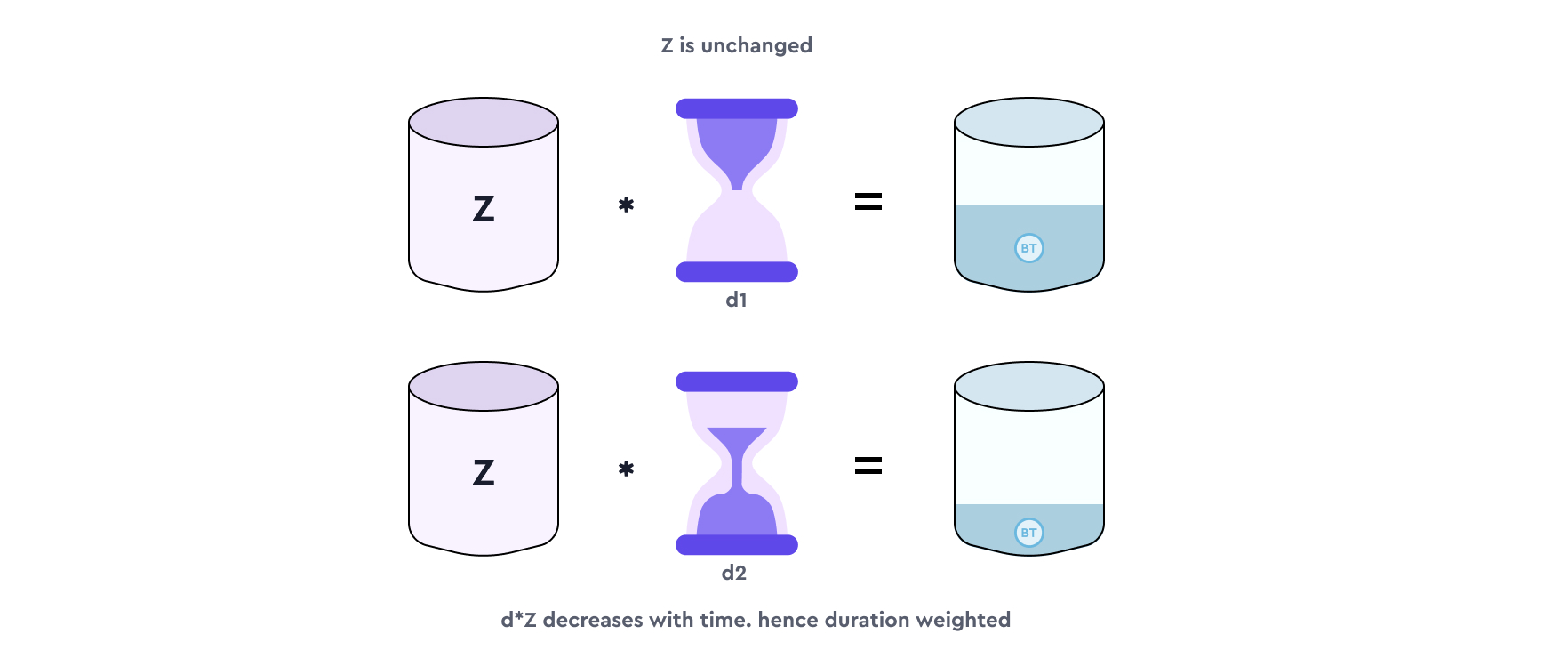
d, representing the remaining duration (in seconds) to pool maturity.
Note that Z represents the interest per second in the AMM. Since d is the remaining duration of the pool, Z*d is the total amount of interest in the pool. While Z changes based on the pool's lending and borrowing activity, d keeps decreasing as d reduces with time.
Timeswap's AMM is duration-weighted as it has a time component (d) in the formula. This assures lenders and borrowers only earn and pay interest for the duration they are interacting with the pool.
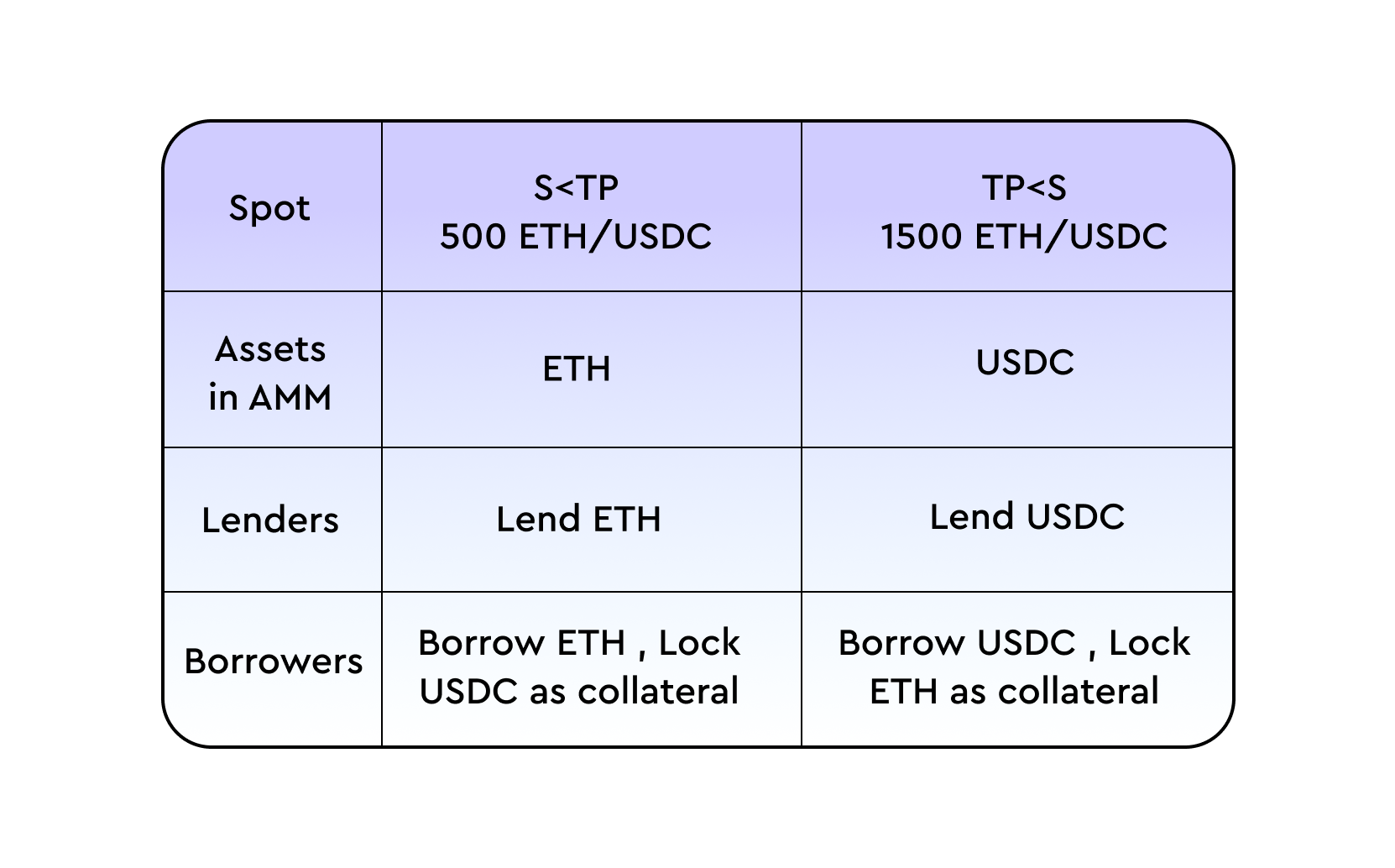
The transition price (TP) of a pool is the ratio at which Token A is to be locked in order to borrow Token B, and vice versa.
Consider an ETH/USDC pool with a TP = 2,000 ETH/USDC. In this pool, borrowers can make either type of transaction, depending on the TP and the spot price:
Deposit 1 ETH to borrow 2,000 USDC
Deposit 2,000 USDC to borrow 1 ETH
This also implies that all the lending transactions in the pool are collateralised by either 2000 USDC or 1 ETH. The TP (along with other initial parameters) is set by the pool creator (the first LP), more details in the Pool Creation page.
Below is a table that summarises the the relationship between TP and spot price, to the characteristic of the pool.
The Timeswap AMM can be broken down into two main components:
Constant Sum Component: (X+Y)
Constant Product Component: (X+Y)*Z
Constant Sum Component: (X+Y)
This component assures overcollateralisation and utilisation of the pools. It allows lenders/borrowers to deposit/withdraw the same amount of X (e.g., 1X = 1 ETH) and Y (e.g., 1Y = 2,000 USDC) at any given time, following the constant sum formula and TP.
According to the constant sum component, X and Y are valued equally within the AMM. This implies that adding either of Token A or Token B will have the same effect on the AMM. Understanding this is crucial because at any given moment, either 1 ETH or 2,000 USDC will be more valuable (depending on the spot price of ETH/USDC). Which means:
Arbitrageurs will always add the less expensive token in the pool to withdraw the more valuable token for profit.
Lenders and LPs on the other hand will always avoid adding the more valuable token in the AMM.
Hence, the AMM can be further broken into two states:
X*Z = K (when Y=0); Price of Y > Price of X In this state, lenders and LPs deposit token X in the pool, which can be borrowed by borrowers.
Y*Z= K (when X=0); Price of X > Price of Y In this state, lenders and LPs deposit token Y in the pool, which can be borrowed by borrowers.
Constant Product Component: (X*Z=K) or (Y*Z=K)
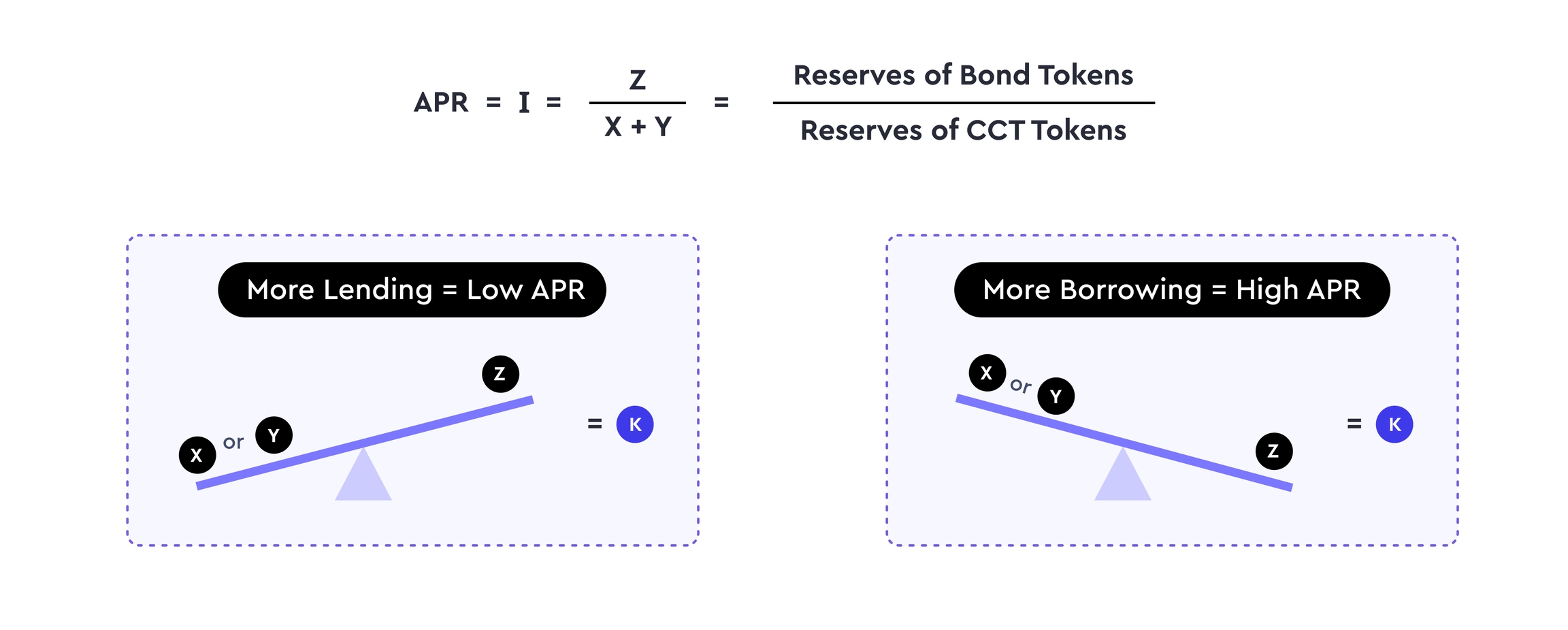
The Constant Product Component helps discover the Interest Rate within the AMM. Similar to the ratio of Y to X in Uniswap V2's AMM, where price discovery happens between buyers and sellers. In Timeswap's AMM, the interest rate discovery happens between lenders and borrowers interacting with the Constant Product component of the AMM.
The interest rate of the AMM is calculated through:
Lenders: Add assets to the AMM in exchange for interest; increasing X (or Y) in the AMM, decreasing Z. This essentially leads to a decrease in the pool's 'I', for the next user.
Borrowers: Add interest to the AMM to borrow assets; increasing Z in the AMM, decreasing X (or Y). This essentially leads to an increase in the pool's 'I', for the next user.
Liquidity Providers: Add both interest and assets to the AMM; increasing X (or Y) and Z to the AMM, in a ratio that does not change the pool's 'I'.
Last updated