Liquidity Provision

As established in the AMM section, X (or Y) refers to the borrowable asset of a pool. Z refers to the interest per second of the pool. Depending on the spot price of the assets and the transition price of the pool, X can be the borrowable asset and Y the collateral asset, or vice versa, in any case, the borrowable asset will always be either X or Y (but not both of them).

Liquidity providers add liquidity into the AMM, and are the counterparty to lenders and borrowers. In return, they earn 10% fees from the interest paid out to lenders and interests paid by borrowers.

LPs are subject to divergence loss/profit, which occurs due to the interest rate spread paid out to lenders and earnt from borrowers. Similar to lenders, LPs also bear the default risk of borrowers not repaying their loans, in which case they receive borrower's forfeited collateral.

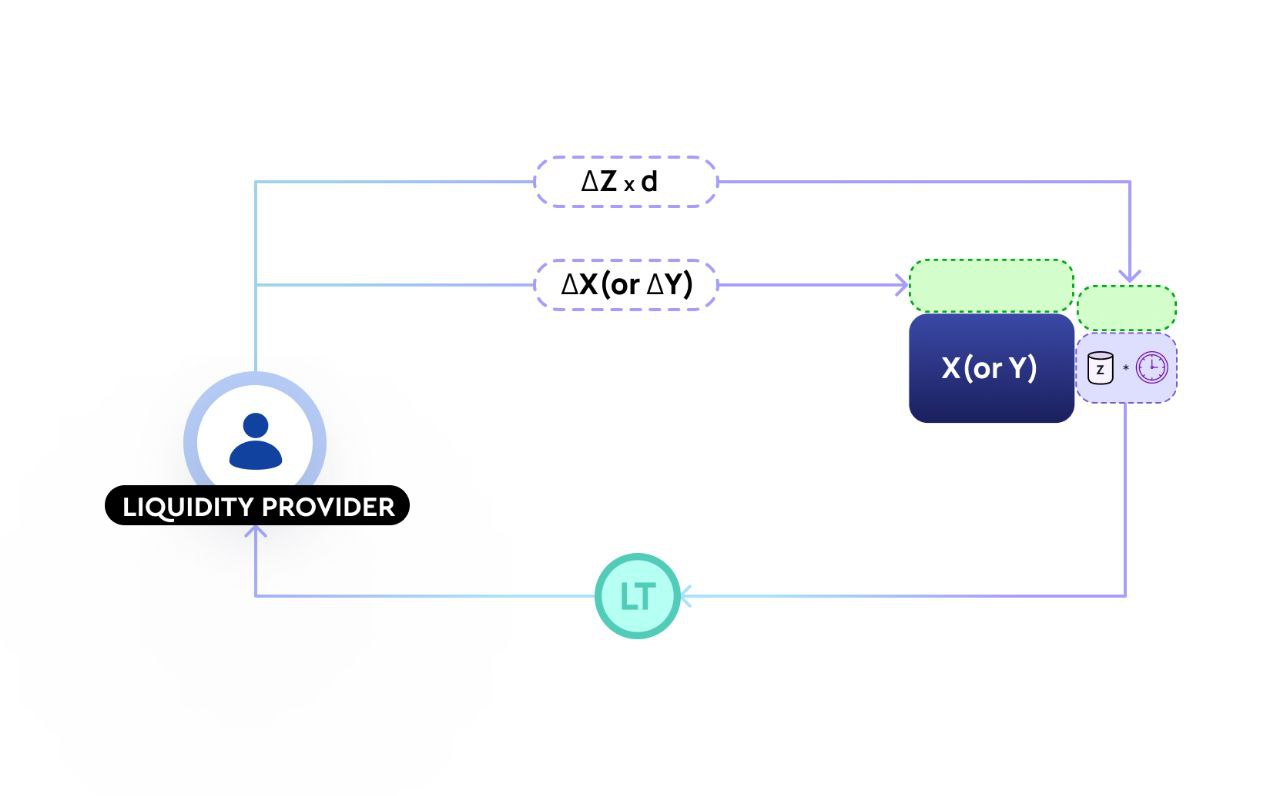
LPs add both X (or Y) and Z to the AMM, in a proportion that does not change the interest rate of the pool.

Providing liquidity

LPs add single asset liquidity in the form of the supplied asset (either X or Y), which depends on the spot price and the TP of the underlying pool.

For example: Consider a USDC/ETH pool with a TP = 2,000 ETH/USDC.

• Case 1: Spot Price (S) = 1,800 ETH/USDC (S < TP) As established from the AMM section, lending/borrowing ETH would make overcollateralised transactions. Hence, LP adds ETH liquidity in the pool.

• Case 2: Spot Price (S) = 2,200 ETH/USDC (S > TP) Similarly, lending/borrowing USDC would be overcollateralised in this case. Leading LPs to add USDC liquidity in the pool.

LP acts as both the lender and borrower of the pool, hence an LP add both X (or Y) and Z in the AMM.

• ΔX+ΔY: The majority of LP's liquidity goes into the constant sum component. This is the lender liquidity of an LP which can be borrowed from the pool. LPs receive BT tokens which represent their claim on the liquidity.

• ΔZ: Smaller portion of the liquidity is added as an Interest amount in the AMM. This is the borrower liquidity of an LP. The interest amount acts as a counterparty to the Lenders who withdraw Interest from the AMM. The divergence loss of an LP is limited to the Interest amount added in the AMM.

A liquidity addition transaction is denoted by the following formula:

$$(X+Y+ΔX+ΔY)(Z+ΔZ)=K+ΔK$$

While the interest rate component is Δz, the actual amount added by the LP is dΔz. It is because the transactions in the pool are duration weighted.

Simply put, Δz is the interest rate per second of the pool, whereas dΔz is the (interest rate)*(duration) for the transaction.

LPs receive Δz amount of BT tokens every second until pool maturity. The Δz amount received over the course of time (every second) will be higher or lower than the amount added by the LP. It is because Δz is the Interest rate of the pool, which changes after every transaction.

For example: Say, Alice adds 1.1 ETH of liquidity in the ETH/USDC pool with the following parameters:

• Interest rate: 10% APR

• Duration: 1 Year (~31557600s)

Here's what the breakdown of the pool liquidity would look like:

• Δx+Δy: 1 ETH (Lender Liquidity)

• dΔz: 0.1 ETH (Borrower Liquidity)

Here, Alice's added 0.1 ETH of Interest in the pool at 10% APR. To recoup this entire amount, she needs the APR to stay 10% on average.

• If the APR averages 5%, she'll receive 0.05 ETH at maturity (+ 1 ETH from the lending side).

• If the APR averages 10%, she'll receive 0.1 ETH at maturity (+ 1 ETH from the lending side).

• If the APR averages 20%, she will get 0.2 ETH at maturity (+ 1 ETH from the lending side).

The 'Average Interest Rate' is what decides the amount

Liquidity Providers receive ERC-1155 Liquidity Tokens (LT) as a receipt of their share of the pool liquidity. The proportion and underlying assets vary with change in I and the relation between the Spot Price and Transition Price.

The exact calculations of the new interest rate (after a liquidity addition transaction) is as follows:

$I=(Z+ΔZ)/(X+Y+ΔX+ΔY)$

Where,

• Z represents the original reserves of interest per second in the AMM

• ΔZ represents the change in interest per second (w.r.t. the AMM), which in this scenario, is positive

• X represents the original reserves of Token A in the AMM

• ΔX represents the change in Token A (w.r.t. the AMM), which in this scenario, is positive

• Y represents the original reserves of Token B in the AMM

• ΔY represents the change in Token B (w.r.t. the AMM), which in this scenario, is positive

Thus, the pool's interest rate remains the same as ratio of Z:(X+Y) is maintained when more liquidity is added.

Fees

Liquidity Providers earn fees from all the transactions that occur in a given pool.

• Borrowers are charged 10% on the interest amount paid (UI reflects the net interest paid by borrowers, including fees).

• Lenders are charged 10% on the interest amount earnt (UI reflects the net interest earnt by lenders, including fees).

Closing a liquidity provision position

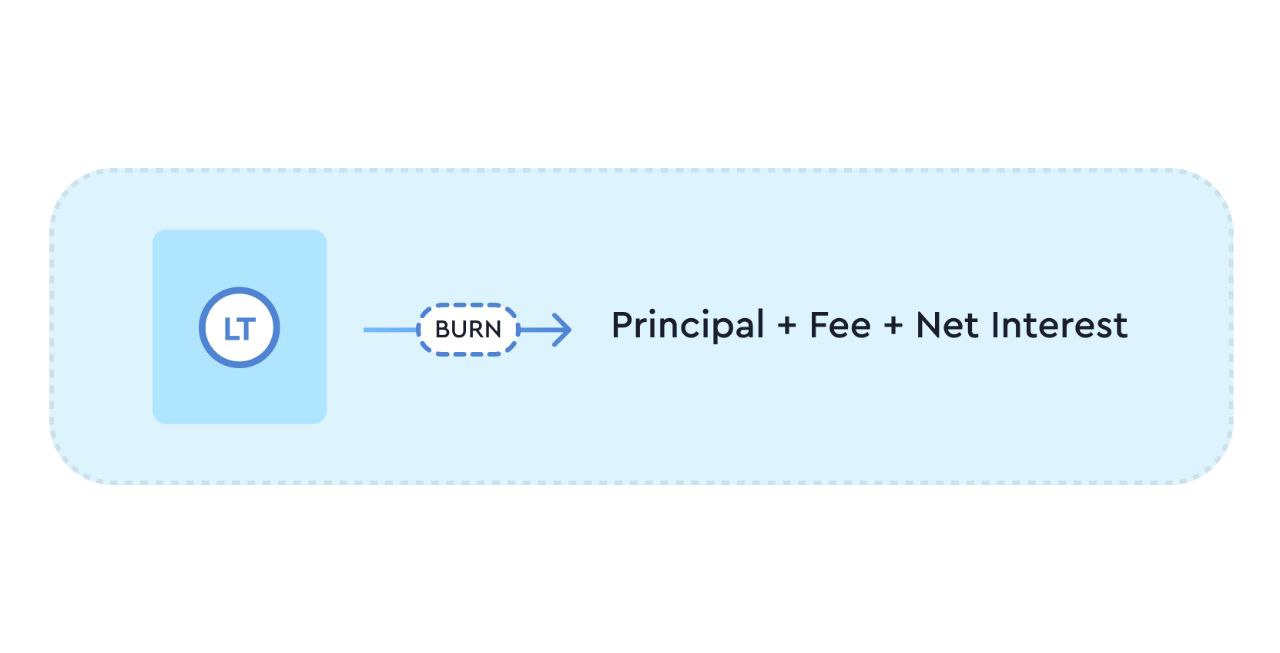
Liquidity Providers can burn their Liquidity Tokens (LT) anytime to withdraw their share of the pool. The amount of tokens received can be different from the amount they added into the pool, depending on the ratio of Z:(X+Y) in the pool.

Here's how a liquidity removal transaction affects the AMM:

$$(X+Y−ΔX−ΔY)(Z−ΔZ)=K−ΔK ​$$

Similar to Liquidity Addition, the Liquidity Removal transaction does not change the Interest Rate in the AMM:

$$I=(Z−ΔZ)/(X+Y−ΔX−ΔY)$$

NOTE: Since the 'Z' amount of interest is withdrawn from the AMM every second, LP also receives some amount of Bond Tokens (BT) separately.

Closing after maturity

Closing LP positions after maturity is very simple given all the lending/borrowing activity has settled and the pool has expired.

Since the 'Z' amount of Bond Tokens are given to LPs every second, there is nothing left in the AMM once the pool has matured. Here's all the tokens received when the Liquidity Tokens (LT) are burned:

• Principal Amount: BT tokens received for the principle added in the (X+Y) section of the AMM are burned to receive the pro-rata amount of Principal + Defaulted collateral.

• Interest Amount: The BT tokens given to the LP every second from the Z component are claimed and burned to receive the pro-rata of Interest + Defaulted collateral.

• Fees earned: The fees paid by lenders and borrowers is in terms of BT tokens which are burned to claim the underlying tokens.

Closing before maturity

Closing a Liquidity position before maturity is not as straight forward at it requires the pool to have existing liquidity, meaning, all of the pool liquidity shouldn't be withdrawn or borrowed already. Interest rate or the ratio of Z:(X+Y) at which liquidity is being removed is crucial to get Divergence loss in your favour.

Suppose Alice added 1.1 ETH of liquidity in the ETH/USDC pool with the following parameters:

• Interest rate = 10% APR

• Duration = 1 year (~31557600s)

Here's what the breakdown of the pool liquidity would look like:

• Δx+Δy: 1 ETH (Lender Liquidity)

• dΔz: 0.1 ETH (Borrower Liquidity)

The LP first burns the ERC-1155 Liquidity Tokens (LT) to withdraw their liquidity from the pool.

Here are the scenario's of Liquidity removal:

Liquidity Removal APR = Liquidity Addition APR

Here, same APR indicates that the ratio of Z:(X+Y) is the same at the time of liquidity removal. Since the tokens are removed at the same ratio, the LP will receive the same amount of tokens.

• Principal Amount: Alice already holds the BT tokens which are now burnt to receive the underlying 1 ETH

• Interest Amount: Since Z amount of BT tokens are given back to the LP every second, the Interest Amount can be broken into two subsegments. 1) Liquidity Addition -> Now The amount of BT tokens received every second from the time of Liquidity addition to Liquidity removal (Now). As we discussed above, this amount depends on the Avg. APR of the Pool for the duration. 2) Now -> Maturity It is the Interest Amount remaining in the AMM. When LPs remove Liquidity before maturity, they withdraw the interest amount from the time of liquidity removal (Now) till Maturity. Thus, removing the liquidity at the same ratio or APR.

• Fees Earned: Fees are also earned in terms of BT tokens and vary depending on the pool volume.

Liquidity Removal APR < Liquidity Addition APR

The APR indicates that the ratio of Z:(X+Y) is different at the time of liquidity removal. Since the tokens are removed at a different ratio, the LP will receive different amounts of tokens. Here, the APR has fallen. (For example: from 10% to 5% APR)

• Principal Amount: Alice already holds the BT tokens, they can now be burnt to receive the underlying 1 ETH

• Interest Amount: Since Z amount of BT tokens are given back to the LP every second, the Interest Amount can be broken into two subsegments. 1) Liquidity Addition -> Now The amount of BT tokens received every second from the time of Liquidity addition to Liquidity removal (Now). Like we discussed above, this amount depends on the Avg. APR of the Pool for the duration. 2) Now -> Maturity It is the Interest Amount remaining in the AMM. When LPs remove Liquidity before maturity, they withdraw the interest amount from the time of liquidity removal (Now) till Maturity. Since the APR has fallen to 5%, Alice will receive the remaining Interest Amount at 5% APR (Half the amount added). This is what leads to divergence loss.

• Fees Earned: Fees is also earned in terms of BT tokens and varies depending on the pool volume.

Liquidity Removal APR > Liquidity Addition APR

The APR indicates that the ratio of Z:(X+Y) is different at the time of liquidity removal. Since the tokens are removed at a different ratio, the LP will receive different amounts of tokens. Here, the APR has increased. (For example: from 10% to 20% APR)

• Principal Amount: Here, Alice can only partially burn her BT tokens to claim a part of the Principal added. This is because the increased APR indicates a larger borrowing demand in the pool, making liquidity scarce. Hence, Alice needs to wait until pool maturity to claim the remaining principal.

• Interest Amount: Since Z amount of BT tokens are given back to the LP every second, the Interest Amount can be broken into two subsegments. 1) Liquidity Addition -> Now The amount of BT tokens received every second from the time of Liquidity addition to Liquidity removal (Now). Like we discussed above, this amount depends on the Avg. APR of the Pool for the duration. 2) Now -> Maturity It is the Interest Amount remaining in the AMM. When LPs remove Liquidity before maturity, they withdraw the interest amount from the time of liquidity removal (Now) till Maturity. Since Alice is removing the liquidity at a 20% APR (double from the initial %), she will receive the double amount of Interest amount from the pool. This is essentially the divergence profit.

• Fees Earned: Fees is also earned in terms of BT tokens and varies depending on the pool volume.

Risks

Apart from the default risk of borrowers not repaying their debts on time (In which case, LPs receive the collateral of the borrowers), LPs also bare the risk of divergence loss.

Divergence Loss: Similar to impermanent loss, the divergence loss is the difference between you HODLing the tokens in your wallet Vs Deploying them into the AMM. On DEXes, divergence loss is calculated by taking the exchange rate between the tokens as a reference. Since Timeswap AMM works for lending/borrowing and has a single token Liquidity Addition, the divergence loss happens by taking the Interest Rate of the market as a reference.

As we reflected above, every LP position has 2 important components to it:

Δx+Δy: It is the total amount of lending principal added into the pool. There is no divergence loss occurring on this principal. At maturity, the BT tokens received can be burnt to claim the principal in full.

dΔz: This is the component of the position which is exposed to Divergence. Whenever there is imbalance in the lend/borrow demand in the pool, the LP(s) find themselves exposed to divergence loss.

Here's the scenario in which the Divergence Loss occurs:

• If the pool APR < LP's APR (APR at which the Liquidity was Added), there will be divergence loss. This is because LP receives Z amount of BT tokens every second. During liquidity addition LP added dΔz at a high APR, whereas now the LP is receiving Z tokens at lower APR.

Here's the scenario in which LP gets Divergence Profit:

• If the pool APR > LP's APR (APR at which the Liquidity was Added), there will be divergence profit. This is because LP the Z amount of BT tokens every second is coming at a higher APR, when compared to the APR at which dΔz was added.

As an LP, one needs to Add liquidity at an interest rate where the lend/borrow demand would stay stable or the borrowing demand would be high.

pagePool Creation