Pool Creation

A pool on Timeswap is first initiated by a Liquidity Provider who sets the initial parameters for the pool. The Pool creator also adds the initial liquidity to bootstrap the market. A liquidity pool can be created for any pair of tokens.

Timeswap can have pools for multiple token pairs, each of which can have different pools with different strike price & maturity dates.

Here's how pools are uniquely identified:

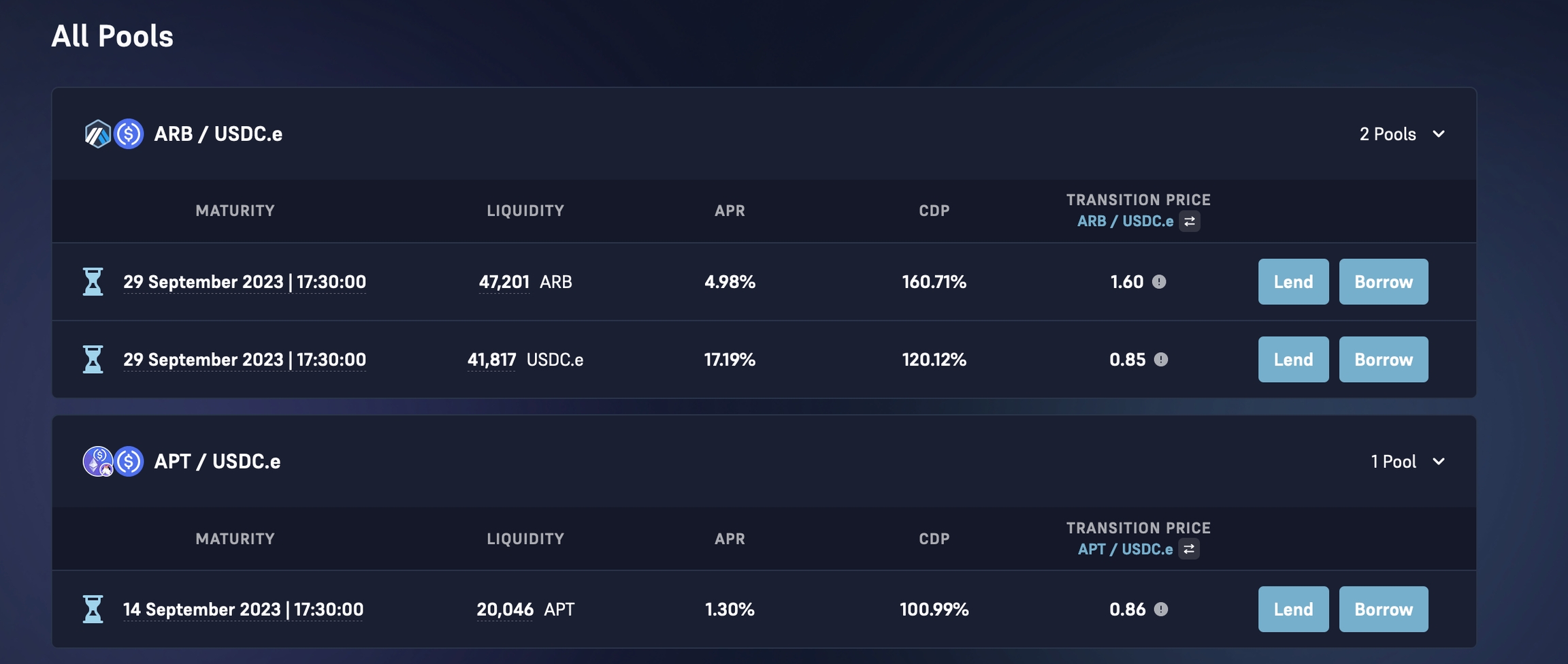
• Token Pair: Defined as Token A/TokenB. (For example: ARB/USDC in the above image.)

• Maturity Date: The date and time at which the pool expires. (For example: 29th September | 17:30:00)

• Transition price: The price level at which borrowers are expected to change their actions (whether to repay or to default on their loans). (For example: 1.60 ARB/USDC)

Now that we understand the Liquidity provider well, it won't be difficult to grasp the pool creator.

Step 1: The Parameters.

Suppose a Liquidity Provider wants to create USDC/ETH pool with the following parameters:

• Interest rate (I): 10% APR

• Transition Price (TP): 1000 USDC per ETH

• Duration (d): 1 Year

Here are some ratios and parameters we would need to create the pool:

$ETH:USDC = 1:1000$

$I=Z/(X+Y)=10/100=(10/100)/d$

Where I is the annual marginal interest rate = 10% annually = 10/100 annually = 1/10

Interest rate per second = (10/100)/d per second (where d is the duration of the pool)

Therefore, $dZ/(X+Y)=1/10$ $dZ:(X+Y)=1:10$ Where dz is the Interest Amount and (x+y) is the amount of tokens available for borrowing. $d=31557600$(seconds in 1 year which is the pool maturity in our example)

NOTE: Liquidity Providers can add any amount of tokens by maintaining Marginal Interest 'I' or $Z:(X+Y)$ ratio.

Depending on the state of the pool, LPs add either ETH (when K>S) or USDC (when S>K). Let's look at both cases.

Step 2: Create Pool.

Case 1: If spot price (S) of ETH<1000 USDC (K) , say 900 USDC per ETH, then the pool parameters will look like this:

$X*Z=K, Y=0$ (Create pool using ETH liquidity)

Initial $X= 10$​ Initial $Y=0$ Initial $Z=1/31557600, (dZ=1)$ (d is 1 yr = 31557600 sec) ​Initial $K = 0.000000316880878$

Now, the above parameters indicate that Liquidity Provider needs 11 ETH (10 ETH for (x+y) & 1 ETH for dz ) in order to create the pool. They can also add less tokens but the ratio of Z:(X+Y) needs to be the same.

The pool creation transaction is as follows:

$(X+Y)*Z=K$ $(10+0)*(1/31557600)=0.000000316880878$

The Marginal Interest rate of the pool is calculated by:

$I=(1/31557600)/(10+0)$

Liquidity provider will receive ERC-1155 Liquidity tokens (LT)

Case 2: If spot price (S) of ETH> 1000 USDC, say 1100 USDC per ETH, then the pool parameters will look like this:

$Y*Z=K, X=0$ (Create pool using USDC)

Initial $X=0$ Initial $Y=10$ Initial $Z= 1/31557600 , (dZ=1)$ (duration of the pool (d) is 1 yr = 31557600 sec) Initial $K= 0.000000316880878$

Now, the above parameters indicate that Liquidity Provider needs a Principal Amount (x+y) of 10,000 USDC (Since y = (10,000 USDC)/(K = 1,000) = 10) and a Interest Amount (dz) of 1,000 USDC to create the pool.

The pool creation transaction is as follows:

$(X+Y)*Z=K$​ $(0+10)*(1/31557600)=0.000000316880878$

The Marginal Interest rate of the pool is calculated by:

$I=(1/31557600)/(0+10)$

Liquidity provider will receive ERC-1155 Liquidity tokens (LT)